Harmonic System Based on the 7 Diatonic Modes
NOTE:
This essay is far from complete, although what shows presently is probably at least something like the way the final essay will begin. But so far, this is intended only for purposes of experimenting with ways of incorporating music examples in text.
In this essay, I would like to describe a possible way of using the seven modes of the diatonic (major) scale. Only six of these were known in ancient times, but in fact there are seven of them - one beginning on each degree of the major scale. One of these was not used owing to its 5th note being a diminished 5th above the tonic note, rather than a perfect 5th, as with all the others.
I will begin by explaining exactly what these modes are, and will then go on to describe some of their characteristics. Finally, I will describe a rather unusual way these modes could be used to build up a whole new harmonic language. To the best of my knowledge, it is of my own devising, although it was influenced by brief passages in Vincent Persichetti's book Twentieth Century Harmony, where he discusses the modes, and gives musical examples of how they might be used - and a couple of these served as the starting point for my own ideas which developed into the harmonic language I will describe here. I have not actually used this system of harmony so far in composition, but I see no reason why it could not be so used.
However, first I must lay some ground-work, and deal with much more elementary matters - and I will try to begin at the very beginning.
Consider the major scale, to begin with. It looks like this in C major, a key which is usually thought of as the central point of the major/minor diatonic harmonic system, because of its lack of either sharps or flats:
C major scale:
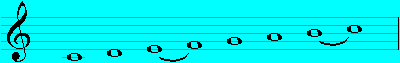
You will notice that two pairs of notes are slurred together. These slurs indicate intervals of a semitone, and I will always mark semitones thus when I notate scales, as it will help show the intervallic structure of various modes and scales, which will be useful in understanding some of what will come later.
Then there is the minor scale. It comes in various forms, but the so-called "natural minor" scale looks like this in A minor:
A natural minor scale:

You will see that it contains exactly the same notes as the C major scale given before, and differs only in that it begins and ends on A, not C. Because scales end on the same note they begin on (although an octave higher, which does not alter its scalic or harmonic function), once you reach the end, you can continue going up another octave, repeating the same notes, and regarding the last note of the first octave as also being the first note of the second octave. In this way, scales can be regarded as cyclic: that is, going round the same series of notes in a circle for as long as you wish, although each recurrence of a note will be an octave higher than the previous instance. (Of course, you could just as easily go round the cycle the other way, which would result in a scale going downwards through one octave after another, instead of upwards. Which direction you go is arbitrary, and doesn't change the essential properties of the scale; however, for the sake of simplicity I will adopt the common convention of treating scales as going upwards in pitch.)
Looking at scales in this way, it can be seen that the A minor and C major scales, as given above, are exactly the same scale, defining that as the circular series of notes that are used, without regard to where you begin and end - and the only difference between these two scales is that a different note is used as a starting and finishing point.
There are two other commonly-recognized forms of the minor scale, namely, the harmonic minor and the melodic minor.
The harmonic minor is like the A minor scale shown above except that the G is sharp; in general, in harmonic minor scales, in whatever key, the 7th note is always raised a semitone higher than it would be in the natural form of the scale. This form of minor scale is called "harmonic minor" because when harmonies are constructed in minor-key music, it often tends to use the raised 7th, especially in dominant harmony. In the A-minor example of a harmonic minor scale just quoted, it is the G# which represents the raised 7th, and dominant harmony would consist of chords containing either E-G#-B or E-G#-B-D.
The melodic minor has an ascending form and a descending form. In the ascending form, both the F and the G are sharp, while the descending form is exactly like the natural form given above. It is called the melodic minor because when melodies are constructed in minor keys, they often tend to incorporate the notes found in either the ascending or descending form of the scale, according to whether the melody is ascending or descending in pitch at the time.
The harmonic minor and melodic minor scales are not of relevance in the following discussion, and will not be referred to any more. The natural minor will continue to be relevant, and, as will be seen, it is also known by another name in a different context. It is presumably called the natural minor scale because it is the basic form of minor scale of which notes are altered to form the harmonic and melodic forms of the scale; and it is presumably this form that is regarded as natural rather than one of the others because it can be considered to derive from the major scale (which comes only in the one form.)
Another point which needs to be disposed of, and left behind: the melodic minor is the only scale which is accepted as having differing ascending and desceding forms. All the other scales I will discuss are the same whether ascending or descending, and for the sake of simplicity, I will consider scales to ascend rather than descend, purely as a commonly accepted convention.
At this point, I want to define two terms quite precisely.
A scale is defined as a particular series of notes arranged in ascending order, and regarded as cyclic. This may not be quite the standard definition of a scale, but it is the one I will always use in all following discussion (except where the context makes it clear I am using the term otherwise, as in conventional expressions such as "C major scale", "A minor scale", and the like). My definition of a scale is the one which is most useful for discussing and analyzing scales, harmonic systems, and the like, and I believe its usefulness justifies this adoption of a slightly unusual (and more precise) definition.
I want to make the following very clear: whenever I talk about scales, I am referring only to a particular set of notes which are to be regarded as cyclic, and I am not regarding any particular note as the starting (and finishing) point. I may go on to consider particular notes as starting points - but simply in defining a particular scale, I am not specifying or assuming any particular note as a starting point.
A mode is the next thing I want to define. A mode is simply a particular scale, starting on a particular note - it is as simple as that.
Therefore, according to these definitions, the C major scale and the A minor natural scale I discussed above are in reality the same scale (at least according to the way I am using these terms), because they both contain exactly the same set of notes. However, because modes include a definition of a starting point within the scale, the A minor and C major scales are different modes of that same scale. (Thus the use of the terms "C major scale" and "A minor scale" does not strictly speaking agree with the way I am using the term "scale". But the distinction between a mode and a scale is too useful to compromise, so I will have to stick to my slightly unorthodox definition of a scale, and will continue to refer to C major scales, A minor scales, and the like, and just accept them as conventional phrases that are not strictly in agreement with my definition of a scale. Fortunately, these conventional concepts of a scale will not figure all that much in this essay, so there shouldn't be any confusion on this point.)
Because I want to divorce the set of notes in the major scale from the major scale as conventionally regarded as beginning on C, I will refer to it as the diatonic scale, not the major scale. "Diatonic" is a musical term which refers to notes which belong to a major or minor scale, as against "chromatic", which refers to notes that don't belong to such a scale, and which therefore require accidentals to notate when they occur in a major- or minor-key passage. It therefore seems fair enough to call the scale made up of those diatonic notes the "diatonic scale".
In doing so, no inference should be drawn as to which note is the starting note for the scale. The reference is merely to the total set of notes used by a musical passage, and the actual starting note, the note which serves as a "tonic" note for the music may be any one of the 7 notes, or there may be no feeling or function of a tonic note at all, and the "tonic" note, if present, may change from time to time within the passage of music. (I have seen the term "pandiatonic" used for music which is based on the diatonic scale, but which has no sense of any particular mode being used, no sense of a "tonic" note.)
Of course, having already considered two different modes of that same diatonic scale (the major and natural minor scales), it may occur to you that one could start on yet other notes, to get yet different modes. The usual system of harmony as used in Western music over the last three centuries or so does not use any modes other than the major or minor scales (the latter in its various forms, according to how it is used).
However, music a couple of centuries earlier than that did use other modes, and in fact it would be putting the cart before the horse to regard these other modes as an extension of the major/minor key system. Rather, the various modes are the basic system, far predating the major/minor key system, which is a later innovation which resulted from the contraction of the earlier modal system. That is, most of the modes gradually fell into disuse a few centuries ago, and only those two we now call the major and minor scales remained in regular use. (That is, C major and A minor, in the examples given above, and various other major and minor keys if the diatonic scale they derive from is transposed to some other pitch. For simplicity, I will, to start with, consider only that pitch at which the diatonic scale is all on white notes as played on a keyboard instrument, or that pitch where no sharps or flats are required for notating various modes. But of course, in reality, the diatonic scale can be used in any of the 12 available transpositions, so that any mode of it can be used beginning on any note. And this fact will be of great importance in the harmonic system based on these modes which I will describe later in this essay.)
Not only did the number of modes in common use decline to just two, but, owing to developments in harmony, the way those two were used changed, so that their manner of usage became less "modal", as the use of chromatic notes increased (something facilitated by the advent of equal temperament).
However, in earlier times, only 6 of the 7 possible modes were used. The one starting on B was not used because its fifth degree (F) is a diminished 5th above the starting note B, unlike all the other modes whose 5th degrees are a perfect 5th above their respective starting notes. (The basic note of a mode, which it both began and ended on, was called the "final" - but I am not going to use that terminology, because the use of modes I will be discussing has very little to do with the ancient use of the modes. I will use the term "tonic" to refer to the starting point of any mode of a particular scale.)
It may be a historical fact that the B-mode was not used when the modal system was current, but it is not relevant in any way to what I will discuss here, and I will treat all seven modes as of equal status. Many text books talking about the ancient modal system do not acknowledge the existence of this "black sheep" mode - a tendency which I must admit irritates me slightly - although historically accurate, it is quite illogical, and in fact the modal system regarded as containing seven modes of equal status has a beautiful symmetry which is completely destroyed if this outcast mode is ignored. Some books which discuss the modes acknowledge the outcast as hypothetically existing, and point out that it was never used because of its diminished 5th, and then say no more about it. These books give it the name of the Locrian mode, although I am not able to establish whether this name was bestowed in recent years by theorists, or whether it was so called in ancient times, even though not used.
Each of the modes has a name which is derived from a region in ancient Greece, where the respective modes were supposedly especially commonly used. (The actual modes the names were attached to in early times are different from the modes they are attached to now. I don't know why the names changed around, and in any case it is completely irrelevant to our purpose here, and I will use exclusively the modern definitions of the various names.)
I will show all 7 modes here, giving their names, and notating all at such a pitch as to require no sharps or flats.
Ionian (C - C):
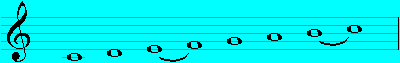
Dorian (D - D):
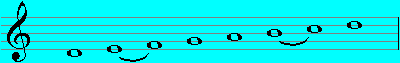
Phrygian (E - E):
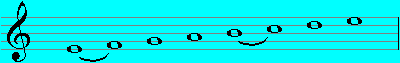
Lydian (F - F):
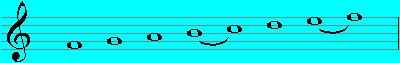
Mixolydian (G - G):
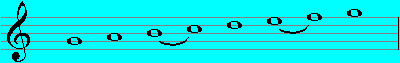
Aeolian (A - A):

Locrian (B - B):
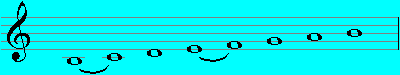
It's easy to see here how the different modes can be derived from the white keys of a piano, just by choosing a different note to start on each time. However, there are other properties of these seven modes I want to explore, which will show up better if we start each mode on the same note, and use accidentals where necessary to give the same pattern of intervals which make each mode distinct from the others. Accordingly, I will notate the modes again in this manner.
But first we have to decide which note to use as the common starting point for the modes, and it would seem preferable to attempt to choose this on a rational basis, rather than just choosing any note randomly. In particular, there are reasons why D would be the best note to choose, and especially why it is a better choice than C, which might seem the obvious choice.
While C is traditionally regarded as the basic note of harmony generally, and the C major scale considered the basic major scale, I am not going to choose C as the note to start the modes on in the following list. There are very good reasons why D is a better note to choose, and this will help bring out the overall symmetry of the modal system more clearly. (Explaining why it will help bring it out would be jumping ahead a bit, but this will become obvious as we go along.)
More generally, there are good reasons (which are covered in another essay) why D can be regarded as the central note of music, and the centre of gravity, not of conventional, non-modal, diatonic harmony (which it is not, C taking that role), but of all possible harmony, of which diatonic harmony is a mere subset. If C is the centre of gravity of diatonic harmony, but D of all harmony, then that simply means that the realm covered by diatonic harmony is not placed centrally within the universal realm of all harmony, but is, so to speak, a little to one side.
I believe this can be demonstrated to be so, but it will take us too far astray to go into that now, and it is not relevant. See Why D is arguably the centre of the harmonic universe, not C [not posted on the site yet] for more detail on this. However, the following will suffice to demonstrate the point for our present purpose: Consider all possible notes, including all natural notes, all sharps and flats, and all double-sharps and all double-flats, but not going into triple-sharps or -flats (if you allow triple-, quadruple-, etc. -sharps and -flats, then the number of notes is infinite, so we will impose the normal limit of double-accidentals); write them out in a long row, left to right, so that they are arranged by ascending perfect 5ths or descending perfect 4ths, this being the usual circle-of-fifths order, and also the order which reflects their harmonic relationship to each other, in terms of the diatonic style of harmony that is common to the modes and to later major/minor tonality. If you do this, you get the following:
Fbb Cbb Gbb Dbb Abb Ebb Bbb Fb Cb Gb Db Ab Eb Bb F C G D A E B F# C# G# D# A# E# B# Fx Cx Gx Dx Ax Ex Bx
That is the full universe of musical notes, adopting the usual limits of double-sharps or -flats.
There are 35 notes there altogether. If you count along from left to right, you will see that D (the 18th note) is in the very middle, not C, and in fact you can see that the entire row of notes has a kind of symmetry around the note D, so its central position is obvious even without counting the notes. Even if you consider just the white notes alone (which we have so far been concerned with in discussing the modes), it can be seen that D is in the centre of the white notes also (F C G D A E B). So there are various ways of seeing D as occupying a more central position in harmony than C, and using D will show certain properties of the modes more clearly than will using C.
So accordingly, I will now list all 7 modes again, this time beginning them all on D. I will also list them in the order that would be required, if they were in their white-note forms, to put their tonics in circle of 5ths order. This also reflects the overall "sharpness" or "flatness" of the notes of the mode relative to the tonic - the Lydian being the "sharpest" and the Locrian being the "flattest".
Lydian (D - D):
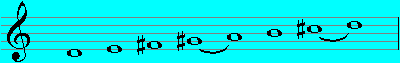
Ionian (D - D):
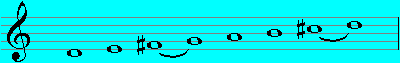
Mixolydian (D - D):
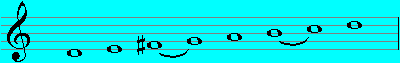
Dorian (D - D):
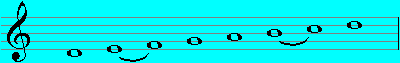
Aeolian (D - D):
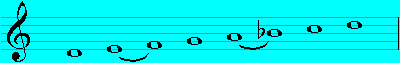
Phrygian (D - D):
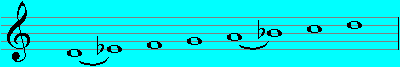
Locrian (D - D):
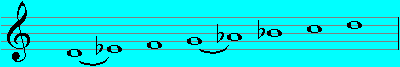
(... not yet finished...)
Original text copyright (C) 2000, 2001, by Michael Edwards.
NOTE ABOUT THE FUTURE OF THIS PAGE - Tuesday, 5 June, 2001:
This page is obviously incomplete, as will be immediately apparent to anyone who reads it through. Please go here for an explanation about the setback that is responsible for my not completing this page, and why it may never be completed, or why it may happen only very slowly. Not that this makes any real difference to someone who would like to see the page complete - but I feel I should at least explain the situation.
I will leave this page here, incomplete as it is, in case the information already written is useful to some readers researching a topic they may have difficulty finding information about on the Internet.
The above is merely an introduction: the greater part of this essay was to consist of a detailed explanation of a new way of using modes within a 20th-century idiom - to explain this, I first of all had to give a detailed description of the modes themselves, which is all that the above does. Then I was going to desscribe various properties of the modes and relationships between them; and then I was going to speculate on some ways one might make use of this in composition - and the above does not even begin cover either of these.
The material that would have made up the rest of this essay has actually already been written, in the form of a letter to a musical friend that I never sent. In order to make it suitable for an essay on this web site, that text needs to be completely revised and its tone made a little more formal (not too much more formal though). I'm afraid I've largely lost the thread of this musical essay, and of others that are already partially written as letters to that friend, and it may be a long time before I pull all the threads of those essays together again; in fact, it is possible that I may never get around to this, but possibly I may be taking an over-pessimistic view of this - but I don't think so.
Introduction - Front page, which leads to Contents
Web Site of Michael Edwards - Contents
Site Map
Writings by Michael Edwards
Music Theory Essays
Harmonic System Based on the 7 Diatonic Modes (this page)
This experimental page created on Saturday, 2 September, 2000;
last modified on Tuesday, 6 August, 2002.